Support » Pololu Jrk USB Motor Controller User’s Guide » 3. Configuring the Motor Controller »
3.d. PID Options
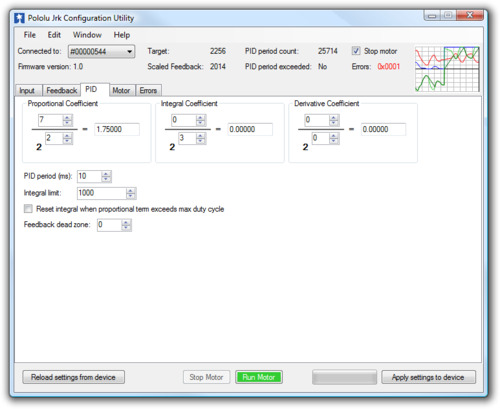 |
The PID tab of the Jrk Configuration Utility |
|---|
The PID tab of the jrk configuration utility controls the central calculation performed by the jrk:
| duty cycle target = | (Proportional coefficient) × error |
| + (Integral coefficient) × integral | |
| + (Derivative coefficient) × derivative |
The integral is computed as the sum of the error over all PID cycles, and the derivative is the current error minus the previous error. The error itself is the difference of the scaled feedback and the target (error = scaled feedback – target). Each of the PID coefficients is specified as an integer value divided by a power of two. The proportional and derivative coefficients can have values from 0.00003 to 1024, and any value above 0.0152 can be approximated within 0.5%. To get the closest approximation to a desired value, type the number into the box after the equal sign, and the best possible numerator and denominator will be computed. In the case of the integral coefficient, the range of the denominator is actually 23 to 218; this is a more useful range, since the integral is usually much larger than the error or derivative.
The PID period can be adjusted here; this sets the rate at which the jrk runs through all of its calculations. Note that a higher PID period will result in a more slowly changing integral and a higher derivative, so that the two corresponding PID constants might need to be adjusted whenever the PID period is changed.
Preventing integral wind-up
Three options are provided for limiting “integral wind-up”, which is the uncontrolled growth of the integral when the feedback system is temporarily unable to keep the error small. This might happen, for example, when the target is changing quickly. One option is the integral limit, a value from 0 to 32767 that simply limits the magnitude of the integral. Note that the maximum value of the integral term can be computed as the integral coefficient times the integral limit: if this is very small compared to 600 (maximum duty cycle), the integral term will have at most a very small effect on the duty cycle.
Another option causes the integral to reset to 0 when the proportional term exceeds the maximum duty cycle parameter. For example, if this option is selected when the proportional coefficient is 15 and the maximum duty cycle is 300, the integral will reset whenever the error is larger than 20.
Additionally the Feedback dead zone option sets the duty cycle target to zero and resets the integral whenever the magnitude of the error is smaller than this amount. This is useful for preventing the motor from driving when the target is very close to scaled feedback. The feedback dead zone uses hysteresis to keep the system from simply riding the edge of the dead zone; once in the dead zone, the duty cycle and integral will remain zero until the magnitude of the error exceeds twice this value.





