Know your units

How many volts of current are there in a bolt of lightning? That’s the kind of stupid question your local news anchor might ask while bantering with the weather guy. Perhaps your favorite cringe-inducing unit abuse is someone thinking light-years measure time or a model rocket enthusiast telling you that a newton-second is a little longer than a regular second. Of course, I made the same class of mistake when looking for a 1-amp battery, which I described in my previous post about battery capacity. That article addressed a specific instance of a general problem: not knowing or understanding units, which allow us to talk about and measure physical properties that we must understand whether we’re designing robots or baking cakes.

There are units for almost every property we care about. For some common properties, such as length or distance, there are many units to choose from; for other properties, there is such a strong connection between the unit and property that the property is called by the unit. For instance, in English, it is common and acceptable to refer to electrical potential as “voltage”; terms like “wattage” and “amperage” are also common but less generally accepted. For other properties, such as torque, there is no common, custom unit; instead, torque is expressed as force multiplied by distance. Part of using units correctly is understanding which of various physically equivalent expressions makes most sense for expressing the idea we want to communicate. Inches per week is a mathematically valid unit for speed, but it is unlikely to be an appropriate unit. A more subtle case of using the correct units for good communication is not over-simplifying a unit. For example, force multiplied by distance also gives us energy, but expressing a torque in joules, the unit for energy, would be counterproductive.

By the way, converting from an incomprehensible quantity in a standard unit to some incomprehensible unit is just dumb. I see this most often in non-engineering contexts, where some understandable unit such as volume is converted to something asinine such as soda cans stacked end-to-end around the equator, or when dollars are converted to miles of stacked one-dollar bills. It can be a fun reality check to estimate the volume or weight of the haul in Ocean’s Eleven, but too often, the numbers are manipulated to exaggerate or obfuscate rather than to enlighten. Sure, big numbers are difficult for us to comprehend, but dump trucks lined up from the earth to the moon are not any better.

Another class of generally useless discussion that comes up in the context of units is arguments about one unit’s superiority over another. This most commonly comes up in the context of the metric system vs. the units used in the United States. While it might be a bit frustrating to have to learn extra units, it’s very easy now (e.g. with Google) to convert them to more familiar ones, and your personal boycott of the inch or meter is not going to make it go away. It’s often convenient to stick with one unit within one calculation or one project, but in general, trying to develop an intuitive sense for more units will only make you more competent as an engineer.

Part of the power of units is the basic math you can do with them. You can multiply and divide any unit by any other unit, and even if you end up with something you can’t quite understand like volts squared or mm⁵, as long as you don’t make a mistake with your math, you can keep going. However you picture a square volt, you can trust that dividing it by a volt will get you back to volts and that dividing by an ohm will get you a watt. This is an important reason to pay attention to the units in all of your calculations: if you end up with the wrong unit, you can be sure something else is wrong with your result. For example, which of these is an expression for the equivalent resistance of two parallel resistors?

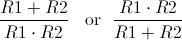If you look at the units, it’s easy to rule out the first candidate since the resulting unit is 1/R, not R as we need it to be.

I’ll probably get to more in-depth discussions of individual units later, plus you can look them up in your physics textbook or Wikipedia, but here are some common groups of units you should at least be aware of:

• Size (distance, area, volume, etc.) - Units for measuring these properties are probably among the most familiar, but because people have been aware of those properties for a long time, there are many alternatives. A consequence of the familiarity (combined with laziness) is that people tend to abbreviate the units, leaving out things like “square” when talking about square feet of area. A more confusing example is copper thickness on circuit boards, which is commonly specified in “ounces”, even though that’s normally a measure of weight. The unit is ounces of copper per square foot, and one ounce corresponds to about 0.0014 inches, or 35 microns. It might be difficult to know what level of abbreviation is appropriate vs. what might be too verbose, but if you’re not familiar or comfortable with a unit, being specific shouldn’t hurt; on the other hand, if everyone around you is saying “square millimeter”, you should not feel free to just call the same thing “millimeter”. Also, mils (thousandths of an inch), which also come up a lot in the context of printed circuit boards, are not short for millimeters.

• Time, rates, frequency - Basic units like seconds should also be very familiar to you, so I’ll just point out that with electronics and programming, we are usually concerned with small fractions of seconds, so you should be comfortable with milliseconds, microseconds, and nanoseconds. We also divide by time to get various rates and frequency, like meters per second, hertz (Hz, or s^-1, or counts per second), and amperes (A, or amps, which are coulombs per second). Sometimes, rates (which are usually some unit divided by time) are instead reported using only the time needed to cover a standard reference amount. For instance, hobby servos could just have their speeds specified in RPM (rotations per minute) or degrees per second, but instead, they are usually specified in terms of how long it takes them to turn 60 degrees. A servo with a “speed” specification of 0.11 seconds can turn 60 degrees in 0.11 seconds, or a full rotation in 0.66 seconds. That’s one and a half rotations per second, or 90 RPM. It’s also worth noting with this example that it’s legitimate to talk about RPM on a device that is not capable of rotating more than a fraction of a rotation, just like you might talk about a rocket car running at 700 miles per hour even though it might not be able to actually travel 700 miles.

• Weight, force, mass - Weight is a another familiar concept even for those who don’t quite know what it means. You should definitely learn how weight, mass, and force are related, but in a practical, robot-building sense (by which I mean staying near the earth’s surface), you probably don’t need to worry (or get up in arms) about whether a pound is a unit of force or a unit of mass. As with other common units, there are a host of unit conversion tools available, so asking someone to convert ounces to grams for you will just make you look lazy. (See how easy it is to convert 5 ounces to grams.)

• Energy, power - Energy can take all kinds of forms, so there are many expressions for it. The basic unit, though, is the joule (abbreviated J), and the basic unit for power, or the rate of energy transfer, is the watt (abbreviated W), which is a joule per second. Watts multiplied by time get you back to energy, and watt-hours might be a more familiar energy unit than joules. So, you can talk about your battery or a cup of gas or the amount of electricity you use in a day in terms of joules or in terms of watt-hours. One horsepower is about 746 watts, so you could talk about having a 1.5 hp microwave oven. You can use energy and power calculations to quickly find all kinds of theoretical limits to your projects, so it’s good to get to know the many expressions for power and energy.

350 F supercap.

• Electrical - Here are a few units that come up a lot in electronics:
  • volts (V) for electrical potential. Voltage is measured between pairs of points, so saying a battery has 9 volts means that one terminal is 9 V higher than the other. There’s no absolute or universal zero reference for voltage, and you can call the most convenient reference point zero V. (A common problem is that some node you think is at zero volts is actually not.)
  • amps (A) for current. Current is a rate (coulombs per second) of electrical charge flowing.
  • ohms (Ω) for resistance. For cases where you want a lot of current flowing (e.g. wires), the resistance is probably under an ohm; if you are putting resistors into your circuit on purpose, they will probably be anywhere from a few ohms to a few megohms.
  • farads (F) for capacitance. A farad is quite big, so most capacitors you will encounter will range from picofarads (pF) to microfarads (uF). However, “supercaps” with many farads are available.
  • henrys (H) for inductance. A henry is also quite big, so most inductors you use in electronics will tend to be in the microhenry (uH) range.

• Torque - Torque comes up a lot with motors, gearboxes, and servos. Torque is expressed as a force multiplied by (i.e. “times”) a distance, so “oz. in.” is pronounced “ounce-inch”, not “ounce per inch” (writing “oz/in” or otherwise introducing any notion of division is just as wrong), and an inch-ounce is the same as an ounce-inch. If you have a torque to start with, the longer the arm on the shaft, the less force you will get at the end of the arm. Conversely, if you are starting with a force, the longer a lever you use, the more torque you can generate. For small robots and toy motors, we usually use ounce-inches or kilogram-centimeters (there are about 13.9 oz. in. per kg-cm); for larger torques, you would see something like pound-feet.

• Temperature - If you’re still reading this, you’re probably already aware of the three main units for temperature: Kelvin (K), Celsius (C), and Fahrenheit (F). A lot of operating ranges for electronics components are specified in C, and the main thing to note for Americans is that something like 150 degrees (F) is not that hot for electronics. If you get into the actual device physics, K starts showing up more.

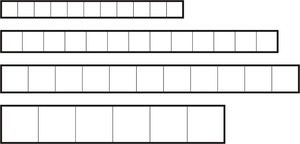If the strips were traces on a PCB, the first and third ones would have the same resistance since each has 11 squares.

• Dimensionless quantities - These aren’t exactly units, but they are related to units, and you should be as comfortable with them as with any unit. dB (decibel), ppm (parts per million), and % (percent) are used for expressing accuracies or ratios between quantities of the same unit. For instance, 1 ppm for 1 MHz is 1 Hz, so a 20 MHz crystal with a 50 ppm specification should be within 1000 Hz of 20 MHz. You should also be familiar with the standard prefixes, like kilo and micro, which just modify other standard units to match the scale of the system being characterized. Finally, you might sometimes see weird units like “per square”, for instance in the context of sheet resistance. In the case of a printed circuit board, once you have a material and thickness specified, you can think of the traces as being built up of squares the width of your trace, and you can think of the resistance based on how many squares make up the trace since a trace that’s twice as wide but twice as long will have the same resistance.