7.2. An example balancing algorithm

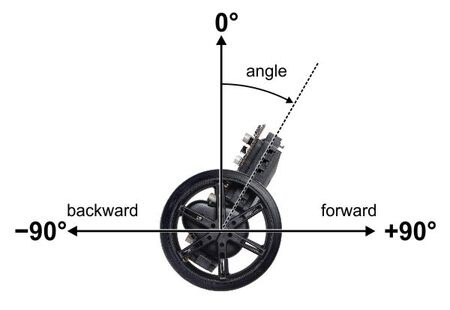Angle convention used by the Balboa 32U4 balancing example.

The gyro measurements we described in the previous section gave us two important variables:

• angle: the angle relative to vertical
• angleRate: the rate of rotation

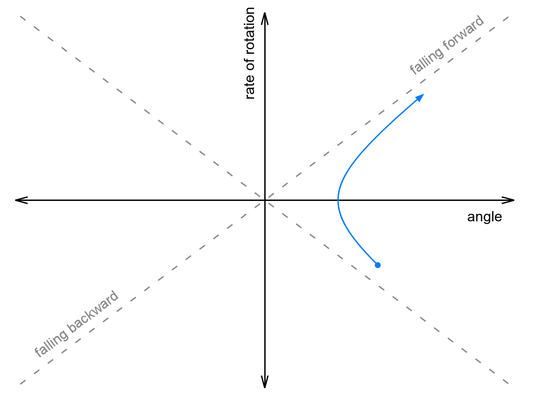
When thinking about these variables, it is helpful to make a plot that shows the trajectory of the robot over time. Suppose we take a Balboa with its motors off, start it leaning forward, and give it a little push toward vertical. Initially, angle is positive and angleRate is negative. As the robot rises toward vertical, angleRate decreases until it runs out of momentum, stops, and starts falling forward. It continues to fall forward, faster and faster, until it hits the floor. The blue curve in the graph below shows approximately what the trajectory looks like:

Now suppose we push it harder, so that it falls over onto its other side. This time, it continues rotating as it passes through vertical, then falls backwards onto the floor:

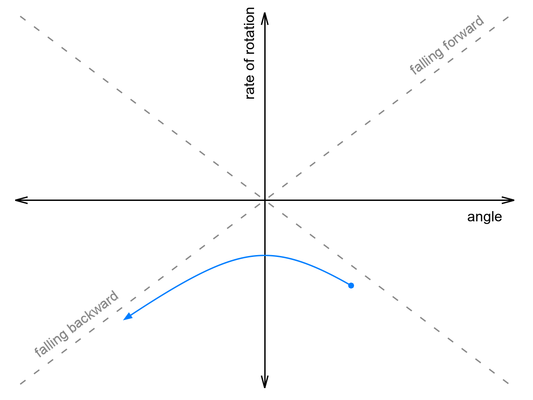Somewhere between these two paths lies a perfectly-balanced trajectory, indicated by the gray dashed line. If we could give it the exact right push, it would follow that line, rising up to vertical just as the rate of rotation falls to zero, and remain balanced forever.

This snippet of code from our Balancer example project computes how far off we are from this ideal rising trajectory:

  // This variable measures how close we are to our basic
  // balancing goal - being on a trajectory that would cause us
  // to rise up to the vertical position with zero speed left at
  // the top.  This is similar to the fallingAngleOffset used
  // for LED feedback and a calibration procedure discussed at
  // the end of Balancer.ino.
  //
  // It is in units of millidegrees, like the angle variable, and
  // you can think of it as an angular estimate of how far off we
  // are from being balanced.
  int32_t risingAngleOffset = angleRate * ANGLE_RATE_RATIO + angle;

In the code, ANGLE_RATE_RATIO is a constant that must be determined through experiment. (A value of 140 worked well for the units we used and our Balboa’s configuration.)

When a Balboa is actively balancing, it “pushes” itself by adjusting the speed of its motors. When the motors make a sudden change in speed, they give a push to the chassis (the combined effect of direct motor torque and of the horizontal motion of the wheels). The effect is the same as if you pushed the chassis by hand: the rate of rotation suddenly changes, in proportion to the change in motor speed.

If you think about it a little, you should see that applying backwards acceleration makes the rate of rotation increase (in the positive direction). So how could a Balboa on a trajectory like the one above save itself? It needs to apply just enough backwards acceleration to bump it up onto that ideal dashed gray line:

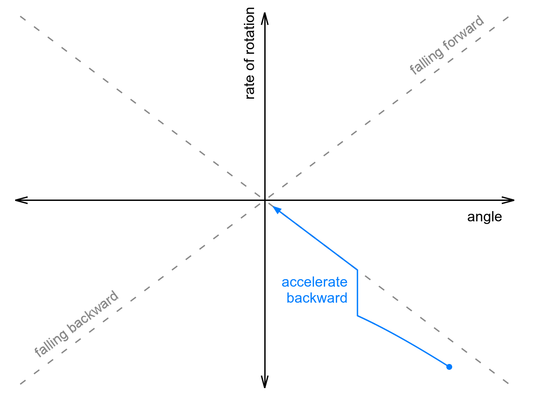We don’t know the exact relationship between acceleration and change in rate of rotation, and acceleration is not actually instantaneous, but the basic point is that we should adjust our motor speed by a factor proportional to the risingAngleOffset variable determined earlier. Here’s approximately how we do that in our code:

  int32_t risingAngleOffset = angleRate * ANGLE_RATE_RATIO + angle;
  motorSpeed += ANGLE_RESPONSE * risingAngleOffset;

In this case ANGLE_RESPONSE is a constant that needs to be adjusted experimentally until the robot can “catch” itself from a variety of starting conditions, ending up as vertical as possible.

But what happens after the robot catches itself? It reached a balanced position by changing the motor speed, so now the motors are driving off in some direction. It is balanced, so there is no reason for it to accelerate or decelerate, and it will drive away until it bumps into something or falls down, which is clearly not ideal behavior.

The Balboa 32U4 includes integrated quadrature encoders that allow a continuous measurement of how fast and far the wheels have turned. We can prevent the robot from driving away by adding additional adjustments to the motor speed that depend on the encoder readings. Counterintuitively, the way to stop it from driving away in one direction is to accelerate even faster in the same direction, causing it to fall back toward where you want to be. Two additional terms are enough to get it to come back to its starting point:

  int32_t risingAngleOffset = angleRate * ANGLE_RATE_RATIO + angle;
  motorSpeed += ANGLE_RESPONSE * risingAngleOffset
    + DISTANCE_RESPONSE * distance
    + SPEED_RESPONSE * speed;

Here distance and speed are our encoder-based measurements of how far the robot is from its starting point and how fast it is going; each variable is multiplied by a constant that must be calibrated experimentally.

The final result is similar to a PID algorithm, but it responds to both rotational and translational motion with a single output, the motor speed. You can probably get similar results just by starting with the angle and distance variables, creating all six possible PID terms, and adjusting their constants to optimize the motion, but it can be hard to get so many constants right at the same time without a clear understanding of what each one means.

The following video shows our balancing algorithm in action. (We did not discuss how to make the robot get up from a lying-down position; see the example code for details.)

The yellow, green, and red LEDs visible in the second part of the video display what the Balboa thinks of its state, with each of the eight possible color combinations indicating a different eighth of the graph. The figure below shows the LED colors in each section of the graph along with the approximate trajectory of the robot after being pushed, so that you can try to follow along with the video:

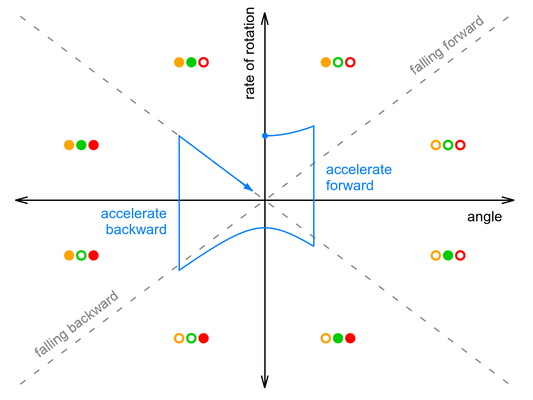One thing you can see from the graph is that the amount of forward acceleration and backward acceleration are about the same, so that overall effect is to drive forward then decelerate to a stop. It’s also important to note that the graph makes it look like the robot only does two large corrections, while in reality it is constantly making small adjustments to the motor speed. It’s actual trajectory might look like a smoothed-out version of the blue line, without sharp corners.

See our Balancer example code for more details and tips on calibration.